library(intsvy) # do złożonych analiz badawczych
library(dplyr) # do manipulacji danymi
library(tidyr) # do przekształcania danych
library(knitr) # do tworzenia ładnych tabel HTML
library(ggplot2) # do wizualizacji danych
# Ustaw ścieżkę do katalogu z danymi
data_path <- "data/PISA/"Analiza tematyczna danych PISA z pakietem intsvy
Ocena różnic w zależności od płci i kraju na umiejętności rozumienia czytanego tekstu; różnice w zależności od kraju i wielkości miejsca zamieszkania na umiejętności w zakresie nauk przyrodniczych; oraz ocena związku statusu społeczno-ekonomicznego z prawdopodobieństwem nieobecności w szkole przez ponad 3 miesiące z powodu problemowych zachowań. W poradniku wykorzystano statystyki opisowe oraz analizy regresji liniowej i logistycznej.
1 Wprowadzenie
Ten dokument przedstawia przygotowanie i analizę danych z badania PISA 2022 (Programme for International Student Assessment 2022) przy użyciu pakietu R intsvy. PISA mierzy umiejętności piętnastolatków niezbędne do sprawnego funkcjonowania w dorosłym życiu: rozumienie czytanego tekstu, umiejętności matematyczne, rozumowanie w naukach przyrodniczych.
Przetestujemy również jak umiejętności rozumowania w naukach przyrodniczych różnią się w zależności od kraju i wielkości miejsca zamieszkania.
Na koniec zbadamy związek między statusem społeczno-ekonomicznym (SES) a nieobecnością w szkole przez ponad 3 miesiące z powodu zachowań problemowych, takich jak przemoc czy używanie narkotyków.
Analiza zostanie przeprowadzona przy użyciu pakietu intsvy, który został zaprojektowany do analizowania złożonych danych badawczych z wagami replikacyjnymi.
Więcej informacji o pakiecie intsvy można znaleźć w naszym poradniku.
2 Konfiguracja
Najpierw załadujemy wymagane pakiety i skonfigurujmy środowisko:
3 Pobieranie, wczytywanie i przygotowanie danych
Dane można pobrać z publicznego repozytorium danych PISA.
Należy pobrać dane w formacie .sav (format danych SPSS) i zapisać je w wybranym katalogu.
Funkcja select.merge() z pakietu intsvy przyjmuje tylko pliki .sav.
Zmienne, na których się skupimy to:
ST004D01T- płeć uczniaCNT- nazwa krajuESCS- wskaźnik statusu społeczno-ekonomicznegoSC001Q01TA- wielkość/typ miejsca zamieszkaniaST261Q02JA- nieobecność w szkole powyżej 3 miesięcy (np.z powodu przemocu, używania lub sprzedawania narkotyków) [Tak/Nie]PV1READdoPV10READ- wartości prawdopodobne wyników rozumienia czytanego tekstuPV1SCIEdoPV10SCIE- wartości prawdopodobne wyników z nauk przyrodniczych
Użyjemy funkcji pisa.select.merge() do wczytania i połączenia zbiorów danych uczniów i szkół. Skupimy się na czterech krajach: Maroko, Finlandia, Singapur i Polska.
pisa22 <- pisa.select.merge(
folder = data_path,
school.file = "CY08MSP_SCH_QQQ.SAV",
student.file = "CY08MSP_STU_QQQ.SAV",
student = c("ESCS", "ST004D01T", "ST261Q02JA"),
school = c("SC001Q01TA"),
countries = c("Finland", "Poland", "Singapore", "Morocco")
)Mamy gotowy zbiór danych do analizy. Przejdźmy dalej.
4 Różnice w wynikach rozumienia czytanego tekstu według kraju i płci
W tej części porównamy średnie i odchylenia standardowe wyników rozumienia czytanego tekstu według kraju i płci.
Średnia i odchylenie standardowe z rozumienia czytanego tekstu według kraju i płci
# Średnie wyniki z rozumienia czytanego tekstu według kraju i płci w PISA
descriptives <- pisa.mean.pv(
pvlabel = paste0("PV", 1:10, "READ"),
by = c("CNT", "ST004D01T"),
data = pisa22
)
kable(descriptives,
digits = 2,
col.names = c("Country", "Gender", "N", "Mean", "Mean s.e.", "SD", "SD s.e."),
align = c("l", "l", "r", "r", "r", "r", "r")
)| Country | Gender | N | Mean | Mean s.e. | SD | SD s.e. |
|---|---|---|---|---|---|---|
| Finland | Female | 4995 | 513.01 | 2.57 | 97.40 | 1.45 |
| Finland | Male | 5244 | 468.32 | 2.77 | 105.49 | 1.36 |
| Morocco | Female | 3401 | 350.37 | 3.94 | 73.63 | 1.97 |
| Morocco | Male | 3466 | 328.65 | 4.21 | 76.01 | 2.15 |
| Poland | Female | 3009 | 503.24 | 3.25 | 98.09 | 2.06 |
| Poland | Male | 3002 | 474.60 | 3.20 | 107.56 | 2.54 |
| Singapore | Female | 3248 | 552.55 | 2.28 | 101.74 | 1.42 |
| Singapore | Male | 3358 | 532.95 | 2.21 | 108.87 | 1.85 |
Pakiet intsvy posiada wbudowane funkcje do tworzenia wykresów dla statystyk opisowych i można ich użyć do wizualizacji wyników.
Umożliwia niewielkie dostosowania wykresów.
desc_plot <- plot.intsvy.mean(descriptives)
desc_plot[["labels"]][["colour"]] <- "Gender"
desc_plot[["labels"]][["x"]] <- "Country"
desc_plot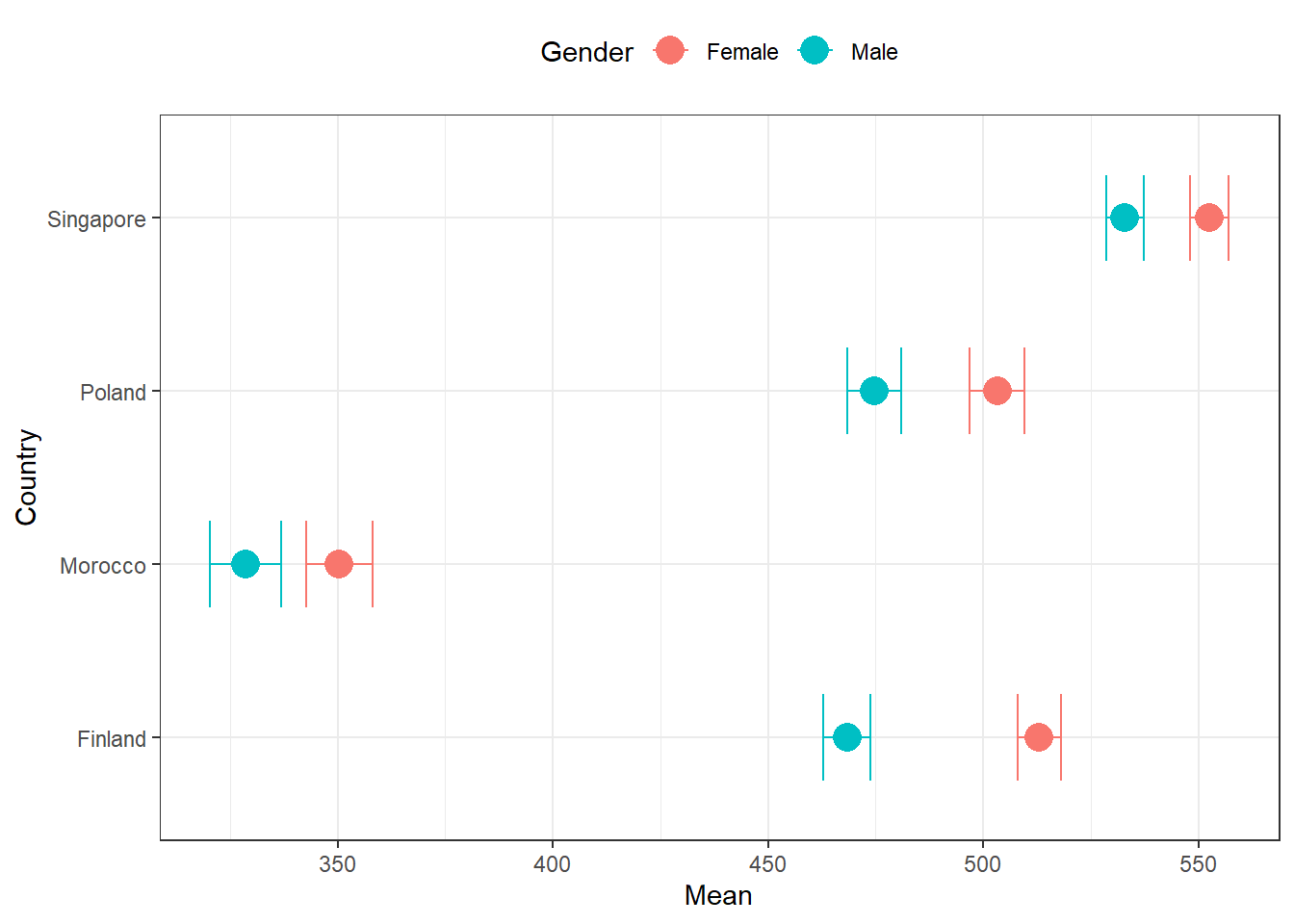
5 Czy umiejętności w zakresie rozumowania w nauk przyrodniczych różnią się w zależności od miejsca zamieszkania?
Na to pytanie odpowiemy za pomocą regresji liniowej, gdzie nauki przyrodnicze będą zmienną zależną, a miejsce zamieszkania zmienną niezależną. Kategoria “wieś, osada lub obszar wiejski (mniej niż 3000 mieszkańców)” będzie kategorią referencyjną.
Rekodowanie zmiennej miejsca zamieszkania
Zmienna miejsca zamieszkania (SC001Q01TA) ma bardzo długie nazwy kategorii.
Dodamy etykiety do tej zmiennej, żeby uzyskać bardziej czytelne wyniki.
kable(with(pisa22, table(SC001Q01TA)))| SC001Q01TA | Freq |
|---|---|
| A village, hamlet or rural area (fewer than 3 000 people) | 2198 |
| A small town (3 000 to about 15 000 people) | 3059 |
| A town (15 000 to about 100 000 people) | 7538 |
| A city (100 000 to about 1 000 000 people) | 8223 |
| A large city (1 000 000 to about 10 000 000 people) | 8003 |
| A megacity (with over 10 000 000 people) | 380 |
pisa22[["SC001Q01TA"]] <- factor(pisa22[["SC001Q01TA"]],
levels = c("A village, hamlet or rural area (fewer than 3 000 people)",
"A small town (3 000 to about 15 000 people)",
"A town (15 000 to about 100 000 people)",
"A city (100 000 to about 1 000 000 people)",
"A large city (1 000 000 to about 10 000 000 people)",
"A megacity (with over 10 000 000 people)"),
labels = c(" Rular <3k",
" Small town 3k-15k",
" Town 15k-100k",
" City 100k-1M",
" Large city 1M-10M",
" Megacity >10M")
)Uruchomienie modelu regresji liniowej
Aby określić, czy predyktor jest istotny, należy wziąć pod uwagę wartości t w wynikach regresji.
Wartości t większe niż 1,96 (w wartości bezwzględnej) wskazują, że predyktor jest statystycznie istotny na poziomie istotności 0,05.
Alternatywnie możemy obliczyć wartość p z wartości t używając następującego wzoru:
wartość p = 2 * (1 - pt(abs(wartość t), df)) gdzie df to liczba wag replikacyjnych minus liczba parametrów do oszacowania.
# Związek miejsca zamieszkania i umiejętności w zakresie nauk przyrodniczych
city_lm <- pisa.reg.pv(
pvlabel = paste0("PV", 1:10, "SCIE"),
x = c("SC001Q01TA"),
data = pisa22
)
# ustaw df do obliczania wartości p
# 80 wag replikacyjnych - 1 (stała) - 5 poziomów czynnika (6-1 (referencja))
dfs <- 80 - 1 - (length(levels(pisa22[["SC001Q01TA"]])) - 1)
city_lm_tab <- city_lm[["reg"]]
city_lm_tab[["p-value"]] <- 2 * (1 - pt(abs(city_lm_tab[["t value"]]), dfs))
city_lm_tab[["p-value"]] <- ifelse(city_lm_tab[["p-value"]] < 0.001,
"<0.001",
round(city_lm_tab[["p-value"]], 3)
)
rownames(city_lm_tab) <- c("Intercept", levels(pisa22[["SC001Q01TA"]])[-1], "R²")
kable(city_lm_tab,
digits = 2,
col.names = c("Variable", "Estimate", "Std. Error", "t-value", "p-value"),
align = c("l", "r", "r", "r", "r")
)| Variable | Estimate | Std. Error | t-value | p-value |
|---|---|---|---|---|
| Intercept | 366.81 | 5.78 | 63.47 | <0.001 |
| Small town 3k-15k | 58.93 | 10.39 | 5.67 | <0.001 |
| Town 15k-100k | 84.18 | 8.27 | 10.19 | <0.001 |
| City 100k-1M | 84.70 | 9.42 | 8.99 | <0.001 |
| Large city 1M-10M | 86.85 | 11.04 | 7.87 | <0.001 |
| Megacity >10M | 15.90 | 19.37 | 0.82 | 0.414 |
| R² | 0.07 | 0.01 | 5.36 | <0.001 |
Pakiet intsvy umożliwia tworzenie wykresów współczynników regresji w ograniczonym zakresie.
Jednak aby stworzyć wykres regresji z predyktorem kategorialnym o kilku poziomach, musimy użyć innego pakietu, takiego jak ggplot2.
Najpierw musimy obliczyć przedziały ufności i dodać kolumnę z kolorem w zależności od kierunku efektu.
city_lm_plot <- city_lm_tab %>%
mutate(
conf.low = Estimate - 1.96 * `Std. Error`,
conf.high = Estimate + 1.96 * `Std. Error`,
color = ifelse(Estimate < 0, "#377EB8", "#E41A1C"),
city = factor(rownames(city_lm_tab), levels = rev(levels(pisa22[["SC001Q01TA"]])[-1]))
) %>%
filter(city != "Intercept" & city != "R²")
city_lm_plot %>%
ggplot(aes(Estimate, city)) +
geom_point(aes(colour = color), size = 3) +
geom_errorbarh(aes(xmin = conf.low, xmax = conf.high, colour = color), linewidth = 1.5, height = 0.2) +
geom_vline(xintercept = 0, lty = 2) +
labs(
x = "Wyniki w naukach przyrodniczych\nw porównaniu do terenów wiejskich (<3k mieszkańców)",
y = "Wielkość miejsca zamieszkania"
) +
scale_colour_manual(values = unique(as.character(city_lm_plot[["color"]]))) +
theme_minimal(base_size = 10) +
theme(legend.position = "none")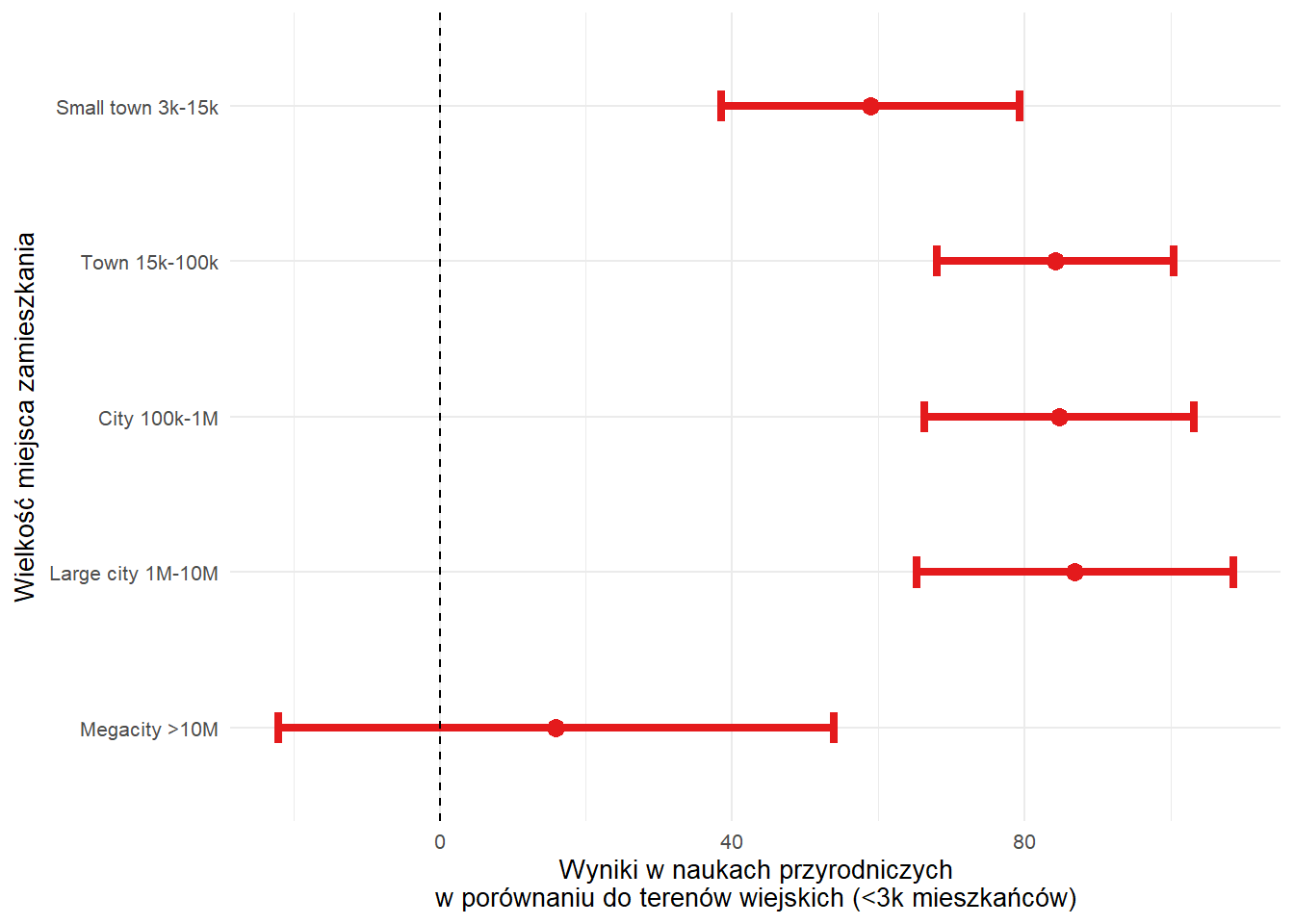
6 SES jako predyktor nieobecności w szkole przez ponad 3 miesiące z powodu zachowań problemowych
W tej części użyjemy regresji logistycznej do sprawdzenia, czy status społeczno-ekonomiczny (SES) przewiduje prawdopodobieństwo nieobecności w szkole przez ponad 3 miesiące z powodu zachowań problemowych.
Tabela krzyżowa dla kraju i interesującej nas zmiennej
Na początku spojrzymy na tabelę krzyżową dla kraju i zmiennej będącej przedmiotem zainteresowania (ST261Q02JA).
cross_tab <- with(pisa22, table(CNT, ST261Q02JA))
kable(cross_tab, digits = 2,
col.names = c("Country", "Yes, n", "No, n")
)| Country | Yes, n | No, n |
|---|---|---|
| Finland | 34 | 250 |
| Morocco | 116 | 812 |
| Poland | 29 | 264 |
| Singapore | 18 | 272 |
prop_tab <- prop.table(cross_tab, margin = 1) * 100
kable(prop_tab, digits = 2,
col.names = c("Country", "Yes, %", "No, %")
)| Country | Yes, % | No, % |
|---|---|---|
| Finland | 11.97 | 88.03 |
| Morocco | 12.50 | 87.50 |
| Poland | 9.90 | 90.10 |
| Singapore | 6.21 | 93.79 |
Odsetek uczniów, którzy opuścili szkołę na 3 lub więcej miesięcy z powodu zachowań problemowych jest stosunkowo niski we wszystkich krajach, ale są zauważalne różnice.
Singapur ma najniższy odsetek (6,2%), podczas gdy w Maroku odsetek ten jest najwyższy (12,5%).
Niemniej jednak chcemy zbadać, czy SES przewiduje zachowania problemowe w tych 4 krajach.
Uruchomienie modelu regresji logistycznej
# Prawdopodobieństwo nieobecności w szkole z powodu zachowań problemowych według SES
escs_log <- pisa.log(
y = "ST261Q02JA",
x = "ESCS",
by = "CNT",
data = pisa22
)
# ustaw df do obliczania wartości p
# 80 wag replikacyjnych - 1 (stała) - 1 (predyktor)
dfs_log <- 80 - 1 - 1
escs_all_log <- do.call(rbind, list(escs_log[["Finland"]][["reg"]],
escs_log[["Morocco"]][["reg"]],
escs_log[["Poland"]][["reg"]],
escs_log[["Singapore"]][["reg"]]
)
)
escs_all_log[["p-value"]] <- 2 * (1 - pt(abs(escs_all_log[["t value"]]), dfs_log))
escs_all_log[["p-value"]] <- ifelse(escs_all_log[["p-value"]] < 0.001,
"<0.001",
round(escs_all_log[["p-value"]], 3)
)
rownames(escs_all_log) <- paste0(rep(c("Finland", "Morocco", "Poland", "Singapore"), each = 2), c(" Intercept", ""))
kable(escs_all_log,
digits = 2,
col.names = c("Variable","Estimate", "Std. Error", "t-value", "Odds Ratio", "lower CI95", "upper CI95", "p-value"),
row.names = TRUE,
align = c("l", "r", "r", "r", "r", "r", "r", "r")
) | Variable | Estimate | Std. Error | t-value | Odds Ratio | lower CI95 | upper CI95 | p-value |
|---|---|---|---|---|---|---|---|
| Finland Intercept | 2.11 | 0.26 | 8.11 | 8.28 | 4.97 | 13.80 | <0.001 |
| Finland | -0.49 | 0.21 | -2.32 | 0.61 | 0.40 | 0.93 | 0.023 |
| Morocco Intercept | 1.27 | 0.16 | 7.91 | 3.56 | 2.60 | 4.88 | <0.001 |
| Morocco | -0.45 | 0.08 | -5.47 | 0.64 | 0.54 | 0.75 | <0.001 |
| Poland Intercept | 2.24 | 0.25 | 8.87 | 9.36 | 5.71 | 15.35 | <0.001 |
| Poland | -0.05 | 0.40 | -0.12 | 0.95 | 0.44 | 2.07 | 0.904 |
| Singapore Intercept | 2.98 | 0.28 | 10.49 | 19.72 | 11.29 | 34.42 | <0.001 |
| Singapore | 0.56 | 0.27 | 2.07 | 1.74 | 1.03 | 2.95 | 0.041 |
Podobnie jak w przypadku wykresu regresji liniowej, dla regresji logistycznej również musimy przygotować wykres samodzielnie używając ggplot2
escs_log_plot <- escs_all_log %>%
mutate(
conf.low = `Coef.` - 1.96 * `Std. Error`,
conf.high = `Coef.` + 1.96 * `Std. Error`,
color = ifelse(`Coef.` < 0, "#377EB8", "#E41A1C"),
country = rownames(escs_all_log)
) %>%
filter(!(endsWith(country, "Intercept")))
escs_log_plot %>%
ggplot(aes(`Coef.`, country)) +
geom_point(aes(colour = color), size = 3) +
geom_errorbarh(aes(xmin = conf.low, xmax = conf.high, colour = color), linewidth = 1.5, height = 0.2) +
geom_vline(xintercept = 0, lty = 2) +
labs(
x = "Związek z nieobecnością w szkole >3 miesięcy\n ze względu na zachowania problemowe",
y = "Kraj"
) +
scale_colour_manual(values = unique(as.character(escs_log_plot[["color"]]))) +
theme_minimal(base_size = 10) +
theme(legend.position = "none")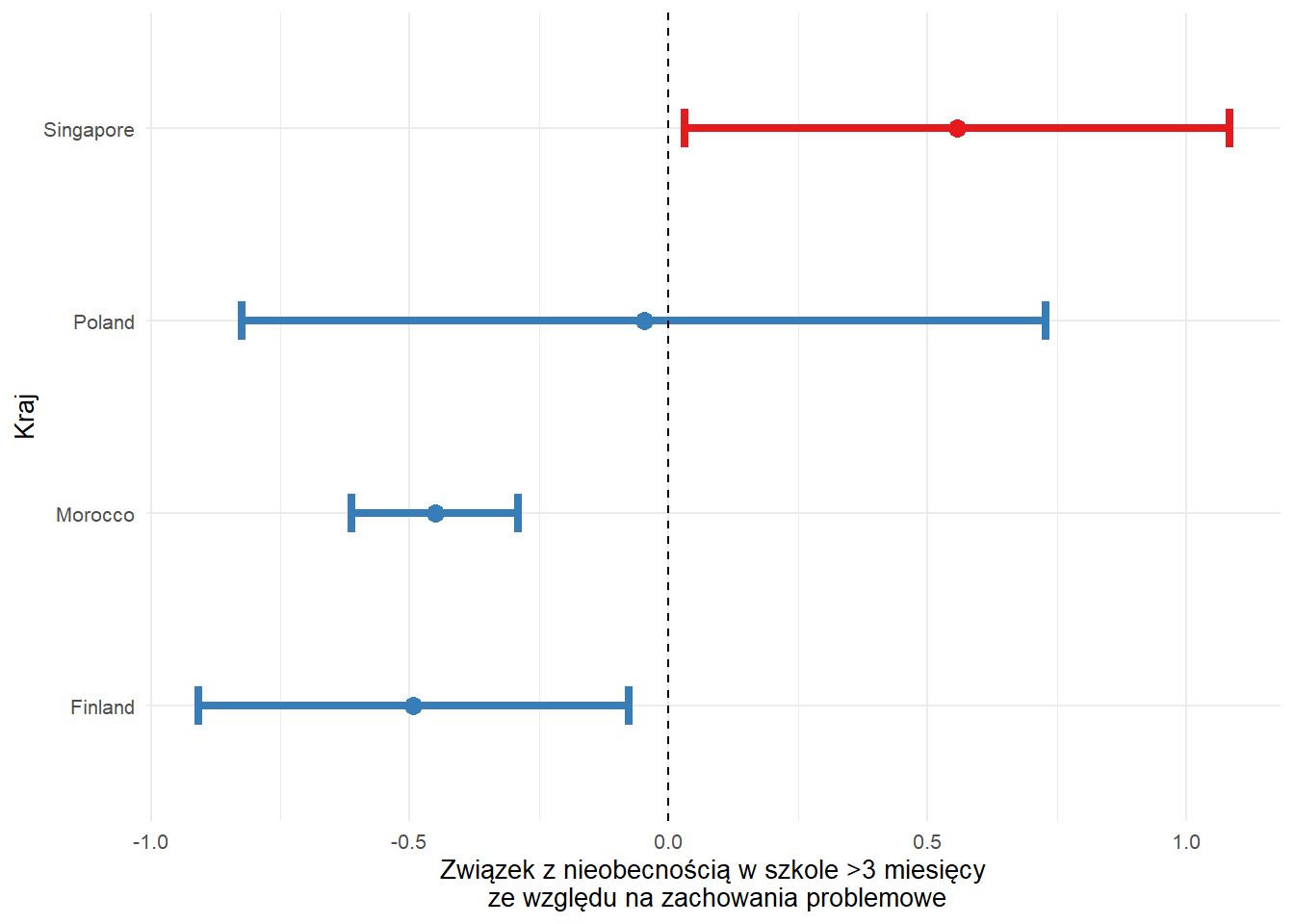
7 Podsumowanie
W tym poradniku przedstawiono, jak przygotować i analizować badanie PISA 2022 za pomocą pakietu R intsvy. Omówiliśmy wczytywanie i łączenie danych oraz obliczenie statystyk opisowych i analiz regresji z uwzględnieniem złożonego schematu badania. Wyniki dostarczyły wglądu w różnice umiejętności czytania według kraju i płci. Następnie zbadaliśmy związek między wielkością miejsca zamieszkania a umiejętnościami w zakresie nauk przyrodniczych. Na koniec zbadaliśmy związek statusu społeczno-ekonomicznego z prawdopodobieństwem opuszczenia szkoły z powodu zachowań problemowych.