Analiza tematyczna danych SSES z pakietem Rrepest

Ocena związku płci, miejsca badania i kohorty wiekowej z samokontrolą i empatią oraz związku SES z wysokim poziomem empatii. W poradniku wykorzystano statystyki opisowe oraz analizy regresji liniowej i logistycznej.

1 Wprowadzenie

Ten dokument prezentuje przygotowanie i analizę danych z badania SSES przeprowadzonego w 2019 roku (Survey on Social and Emotional Skills Round 1) przy użyciu języka R. SSES 2019 była pierwszą edycją międzynarodowego badania edukacyjnego mającego na celu ocenę umiejętności społecznych i emocjonalnych uczniów w wieku 10 i 15 lat.
Przedstawiona tutaj analiza koncentruje się na różnicach związanych z płcią, miejscem badania i kohortą wiekową w zakresie samokontroli oraz na związku między statusem socjoekonomicznym (SES) a wysoką empatią.
Będziemy używać bazy danych uczniów (students dataset), koncentrując się na następujących miejscach badania: Bogota, Helsinki i Moskwa.

2 Przygotowanie środowiska

Najpierw załadujemy wymagane pakiety i przygotujemy nasze środowisko pracy

library(haven) # do wczytywania plików .dta Stata
library(dplyr) # do manipulacji danymi
library(tidyr) # do przekształcania danych
library(labelled) # do usuwania etykiet zmiennych
library(Rrepest) # do złożonych analiz badań międzynarodowych
library(knitr) # do tworzenia ładnych tabel html
library(ggplot2) # do wizualizacji danych

# Ustaw ścieżkę do katalogu z danymi
data_path <- "data/SSES/"

# Ustaw wektor z nazwami kolumn zawierających wagi replikacyjne
weights_vec <- paste0("rwgt", 1:76)

3 Pobieranie i wczytywanie danych

Pobieranie danych

Dane można pobrać z publicznego repozytorium danych SSES 2019.
Musisz pobrać plik INT_01_ST_(2021.04.14)_Public.dta (format danych Stata) z publicznego repozytorium danych SSES 2019 i umieścić go w wybranym katalogu.
Plik .sav (format danych SPSS) jest dostępny, ale w zbiorze danych uczniów w formacie .sav brakuje jednej wagi replikacji (rwgt9), więc nie możemy przeprowadzić analizy z jego użyciem.

Zmienne, na których się skupimy to:

• Gender_Std - płeć ucznia (1 = kobieta, 2 = mężczyzna)
• CohortID - kohorta uczniów (1 = 10 lat, 2 = 15 lat)
• SiteID- numer identyfikacyjny miejsca badania
• SES - wskaźnik statusu społeczno-ekonomicznego
• SEL_WLE_ADJ - wynik samokontroli
• EMP_WLE_ADJ - wynik empatii

Wczytamy surowe pliki danych i wybierzemy tylko zmienne potrzebne do analizy:

# Wczytaj surowe dane 
student_data <- read_dta(paste0(data_path, "INT_01_ST_(2021.04.14)_Public.dta"))

# Zdefiniuj zmienne do zachowania 
student_vars <- c("Username_Std", "Username_TC", "SiteID", "Gender_Std", "CohortID",
                  "SEL_WLE_ADJ", "EMP_WLE_ADJ", "SES", weights_vec, "WT2019")

4 Manipulacja danymi przy użyciu dplyr

Pakiet dplyr używa funkcji połączonych za pomocą operatora pipe (%>%).

Więcej o operatorze pipe można przeczytać tutaj:

Dokumentacja funkcji pipe
Rozdział “Pipes” w “R for Data Science”

# Wybierz tylko mężczyzn i kobiety
sses_data <- student_data %>%
  filter(Gender_Std %in% c(1,2))

# Wybierz kolumny (zmienne) potrzebne do analizy
sses_data <- sses_data %>%
  select(all_of(student_vars))

# Wybierz tylko 3 miejsca i przekształć zmienne
sses_data <- sses_data %>%
  filter(SiteID %in% c("01", "03", "07")) %>% # Wybierz Bogotę, Helsinki i Moskwę
  mutate(
    # Utwórz zmienną z nazwami miejsc badania zamiast identyfikatorów
    SiteName = case_when(
      SiteID == "01" ~ "Bogota",
      SiteID == "03" ~ "Helsinki",
      SiteID == "07" ~ "Moscow"
    ),
    # Zmień Gender na zmienną nominalną 
    Gender_Std = if_else(Gender_Std == 1, 0, 1),
    Gender = if_else(Gender_Std == 0, "Female", "Male"),
    CohortID = if_else(CohortID == 1, 0, 1),
    Cohort_name = if_else(CohortID == 0, "10 lat", "15 lat")
  )

# Usuń etykiety 
sses_data <- remove_labels(sses_data)

Mamy zbiór danych gotowy do analizy. Przejdźmy dalej.

5 Różnice w samokontroli między miejscami badania i płciami

W tej części porównamy średnie i odchylenia standardowe wyniku samokontroli (SEL_WLE_ADJ) według miejsca badania i płci.

Poniżej znajduje się opis użycia funkcji Rrepest() z pakietu Rrepest:

Opis często używanych argumentów Rrepest():

• argument svy określa projekt badania
  
• argument by pozwala na grupowanie według wielu zmiennych
  
• argument est określa statystyki do obliczenia (np. średnia, odchylenie standardowe);
  
• argument target określa zmienną, dla której obliczane są statystyki (np. SEL_WLE_ADJ dla samokontroli)

Adnotacja

Więcej informacji o pakiecie Rrepest można znaleźć w naszym tutorialu.

Średnia i odchylenie standardowe samokontroli według miejsca badania i płci

# oblicz statystyki opisowe
desc_results <- Rrepest(sses_data,
        svy = "SSES",
        by = c("SiteName", "Gender"),
        est = est(c("mean", "std"), target = "SEL_WLE_ADJ")
)

# wyświetl tabelę
kable(desc_results,
  digits = 2, 
  col.names = c("Site", "Gender", "Mean", "Mean s.e.", "SD", "SD s.e."),
  align = c("l", "l", "r", "r", "r", "r")
  )

Site	Gender	Mean	Mean s.e.	SD	SD s.e.
Bogota	Female	578.07	1.50	90.11	2.25
Bogota	Male	559.93	1.88	85.02	1.85
Helsinki	Female	581.43	2.00	94.14	2.40
Helsinki	Male	578.30	2.09	92.61	1.74
Moscow	Female	564.53	1.68	89.00	1.57
Moscow	Male	577.64	1.66	93.39	1.67

Możemy również przedstawić wyniki na wykresie słupkowym:

# wykres słupkowy
desc_results %>%
  ggplot(aes(x = SiteName, y = b.mean.sel_wle_adj, fill = Gender)) +
  geom_bar(stat="identity", color="black", position=position_dodge()) + 
  scale_fill_brewer(palette="Set1") +
  xlab("Miejsce badania") +
  ylab("Średni wynik samokontroli") +
  theme_minimal(base_size = 14)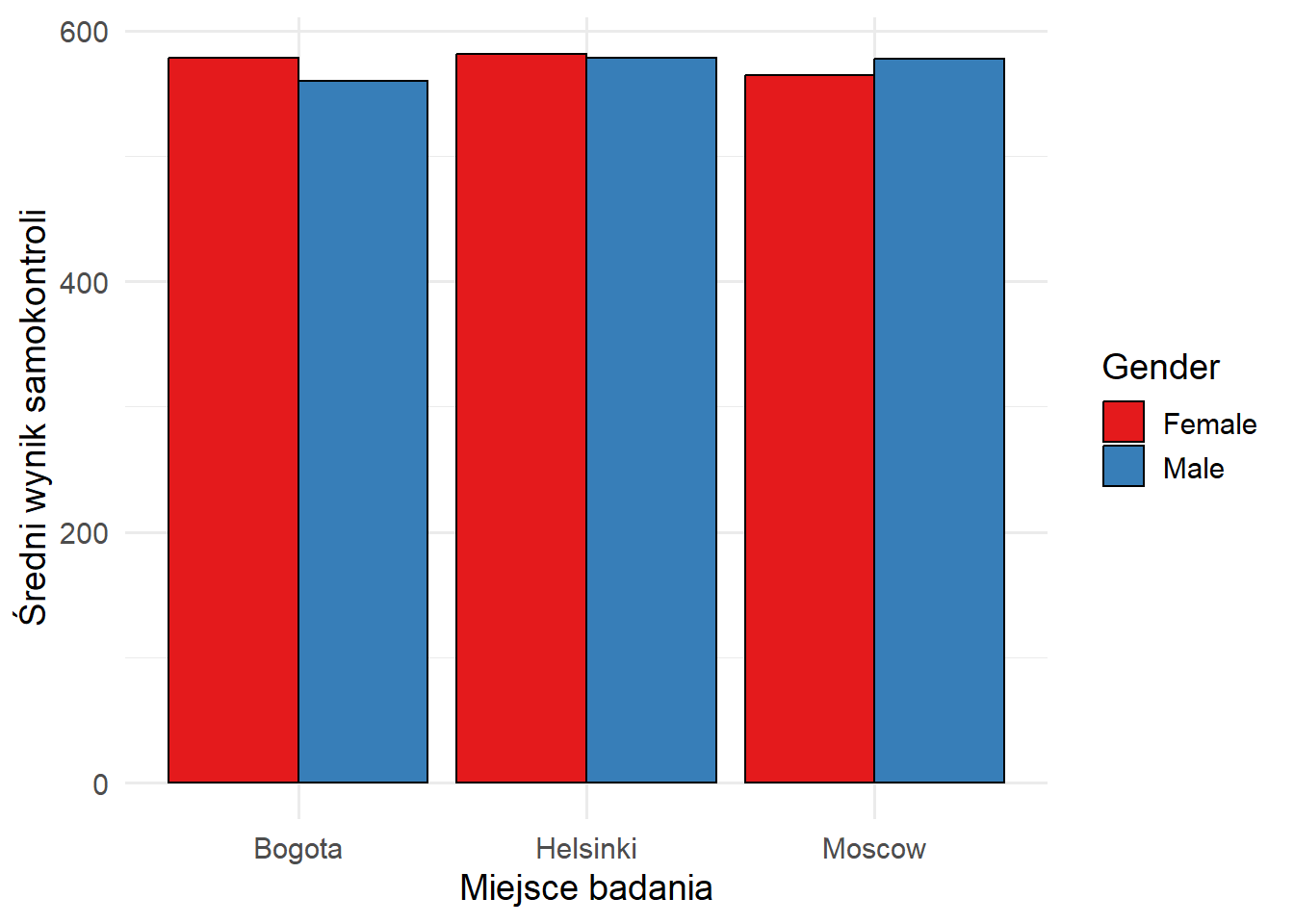

Interpretacja

W Bogocie i Helsinkach średni wynik samokontroli był wyższy dla dziewcząt (Bogota - 578, Helsinki - 581) niż dla chłopców (Bogota - 560, Helsinki - 578). W Moskwie sytuacja jest odwrotna - chłopcy uzyskali wyższy wynik (578) niż dziewczęta (565).

6 Czy samokontrola różni się między kohortami wiekowymi?

Na to pytanie odpowiemy używając regresji liniowej, z samokontrolą jako zmienną zależną i kohortą wiekową (10 vs 15 lat) jako predyktorem.

Używając Rrepest:

• Wykonamy ważoną regresję liniową
  
• Wyodrębnimy i sformatujemy współczynniki regresji, błędy standardowe i statystyki R-kwadrat
  
• W celu testowania hipotez obliczymy statystyki t ręcznie

Testowanie istotności statystycznej

Aby określić, czy predyktor jest istotny statystycznie, powinniśmy oprzeć się na wartościach t w tabeli regresji.
Wartości t większe niż 1,96 (w wartości bezwzględnej) wskazują, że predyktor jest statystycznie istotny na poziomie istotności 0,05.

Alternatywnie możemy obliczyć wartość p z wartości t używając następującego wzoru:
p-value = 2 * (1 - pt(abs(t-value), df)) gdzie df (stopnie swobody) to liczba wag replikacyjnych minus liczba parametrów do oszacowania.  

Aby obliczyć statystykę t dla tabeli regresji, musimy ustawić liczbę stopni swobody.
Stopnie swobody są równe liczbie wag replikacyjnych minus liczba oszacowanych parametrów.
W obu analizach regresji mamy dwa parametry: stałą i 1 predyktor (kohorta wiekowa).

n_dfs <- 76 - 2

Uruchom model regresji liniowej

lm_results <- Rrepest(data = sses_data,
        svy = "SSES", 
        by = "SiteName",
        est = est("lm", 
                  target = "SEL_WLE_ADJ", 
                  regressor = 'CohortID'))

Następnie utworzymy sformatowaną tabelę regresji używając dplyr i tidyr:

# przekształć tabelę wyników
lm_reshaped <- lm_results %>%
  pivot_longer(
    cols = -SiteName,
    names_to = c("stat_type", "parameter"),
    names_pattern = "^(b\\.|se\\.)reg_sel_wle_adj\\.(.+)$",
    values_to = "value"
  ) %>%
  mutate(
    stat_type = case_when(
      stat_type == "b." ~ "Estimate",
      stat_type == "se." ~ "SE"
    ),
    parameter = case_when(
      parameter == "intercept" ~ "Intercept",
      parameter == "cohortid" ~ "Cohort age",
      parameter == "rsqr" ~ "R²"
    )
  ) %>%
  pivot_wider(
    names_from = stat_type,
    values_from = value
  ) %>%
  select(SiteName, parameter, Estimate, SE) %>%
  mutate(
    t_value = Estimate / SE,
    conf.low = Estimate - 1.96 * SE,
    conf.high = Estimate + 1.96 * SE,
    p_value = 2 * pt(abs(t_value), n_dfs, lower.tail = FALSE),
    p_value = ifelse(p_value < 0.001, "<0.001", format(round(p_value, 3), digits = 3, nsmall = 3))
    )
    
# przekształć dla wykresu
lm_for_plot <- lm_reshaped %>%
  filter(parameter == "Cohort age") %>%
  select(SiteName, Estimate, SE, conf.low, conf.high) %>%
  mutate(
    color = ifelse(Estimate < 0, "#377EB8", "#E41A1C")
  )
# przekształć dla tabeli html
lm_reshaped <- lm_reshaped %>%
  mutate(
    SiteName = ifelse(duplicated(SiteName), "", SiteName),
    conf.low = ifelse(conf.low > -0.01 & conf.low < 0, "<0", format(round(conf.low, 2), digits = 2, nsmall = 2)),
    conf.high = ifelse(conf.high < 0.01, "<0.01", format(round(conf.high, 2), digits = 2, nsmall = 2))
  )
  
# wyświetl tabelę
kable(lm_reshaped,
  digits = 2,
  col.names = c("Site", "Parameter", "Estimate", "Std. Error", "t value", "lower CI", "upper CI", "p-value"),
    align = c("l", "l", "r", "r", "r", "r", "r", "r")

)

Site	Parameter	Estimate	Std. Error	t value	lower CI	upper CI	p-value
Bogota	Intercept	573.56	1.89	304.13	569.86	577.25	<0.001
	Cohort age	-8.87	2.86	-3.10	-14.47	<0.01	0.003
	R²	0.00	0.00	1.58	<0	<0.01	0.119
Helsinki	Intercept	591.82	2.84	208.39	586.26	597.39	<0.001
	Cohort age	-25.98	3.38	-7.69	-32.60	<0.01	<0.001
	R²	0.02	0.00	4.05	0.01	0.03	<0.001
Moscow	Intercept	571.95	2.07	275.76	567.89	576.02	<0.001
	Cohort age	-1.55	2.78	-0.56	-7.00	3.90	0.579
	R²	0.00	0.00	0.27	<0	<0.01	0.786

Poniżej znajduje się wykres pokazujący wartości współczynników modelu regresji i 95% przedziały ufności dla związku kohorty wiekowej z samokontrolą według miejsca przeprowadzenia badania.
Wszystkie współczynniki są ujemne, więc użyto koloru niebieskiego.
Można zobaczyć, że dla Bogoty i Helsinek przedziały ufności nie zawierają zera, więc efekt kohorty wiekowej w tych dwóch miastach jest istotny.
Dla Moskwy przedział ufności przecina zero, więc efekt nie jest istotny.

# wykres oszacowań regresji liniowej
lm_for_plot %>%
  ggplot(aes(Estimate, SiteName)) +
  geom_point(aes(colour = color), size = 3) +
  geom_errorbarh(aes(xmin = conf.low, xmax = conf.high, colour = color), linewidth = 1.5, height = 0.2) + 
  geom_vline(xintercept = 0, lty = 2) +
  labs(
    x = "Współczynnik efektu wieku na samokontrolę (15-latkowie vs 10-latkowie)",
    y = "Miejsce badania"
      ) +
  scale_colour_manual(values = unique(as.character(lm_for_plot[["color"]]))) +
  theme_minimal(base_size = 9) +
  theme(legend.position = "none")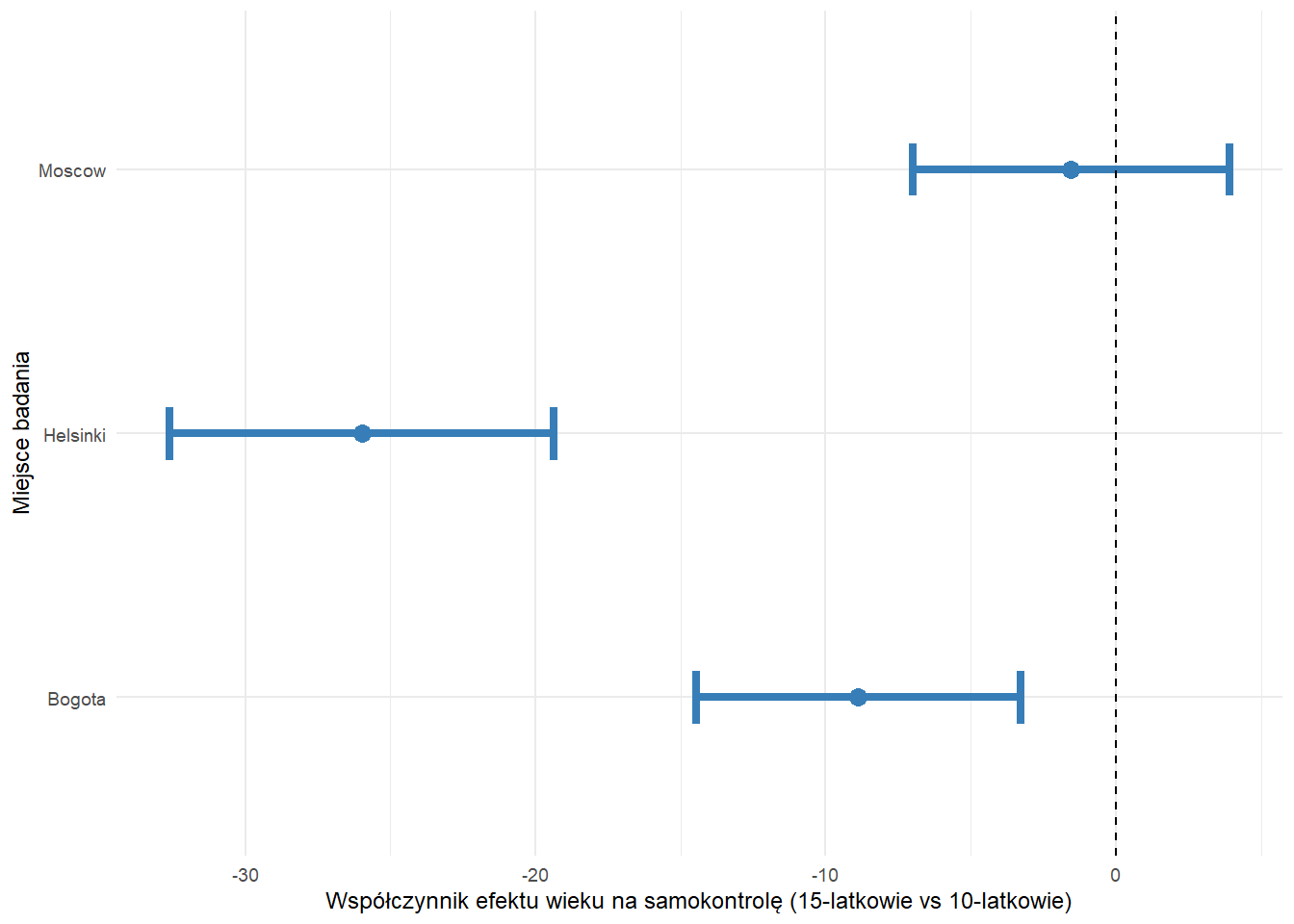

Interpretacja

Wyniki pokazują, że kohorta wiekowa uczniów (15-latkowie vs 10-latkowie) jest istotnym predyktorem samokontroli w Bogocie i Helsinkach, ale nie w Moskwie. Młodsza kohorta uzyskała wyższy wynik samokontroli w tych dwóch miastach. Jednocześnie wartości R-kwadrat wskazują, że tylko model dla Helsinek wyjaśnia znaczącą część wariancji w wynikach samokontroli (R-kwadrat = 0,02, wartość p < 0,001).

7 SES jako predyktor wysokiej empatii

W tej części wykorzystamy regresję logistyczną, aby zbadać, czy status społeczno-ekonomiczny (SES) przewiduje wysoką empatię (EMP_WLE_ADJ). Zdefiniujemy wysoką empatię jako wynik powyżej 90. percentyla rozkładu wyników empatii.

Utworzenie zmiennej nominalnej dla wysokiej empatii i przeprowadzenie regresji logistycznej

# Obliczenie 90. percentyla wyniku empatii 
emp_90 <- quantile(sses_data$EMP_WLE_ADJ, 0.9, na.rm = TRUE)

# Utworzenie zmiennej norminalnej dla wysokiej empatii
sses_data[["emp_90_bin"]] <- ifelse(sses_data[["EMP_WLE_ADJ"]] < emp_90, 0, 1)

# Uruchomienie regresji logistycznej
log_results <- Rrepest(
  data = sses_data,
  svy = "SSES",
  est = est("log", 
            target = 'emp_90_bin',
            regressor = "SES"),
  by = "SiteName"  
)

Tak samo jak wcześniej, utworzymy sformatowaną tabelę regresji używając dplyr i tidyr:

# przekształć tabelę wyników
log_reshaped <- log_results %>%
  pivot_longer(
    cols = -SiteName,
    names_to = c("stat_type", "parameter"),
    names_pattern = "^(b\\.|se\\.)log_emp_90_bin\\.(.+)$",
    values_to = "value"
  ) %>%
  mutate(
    stat_type = case_when(
      stat_type == "b." ~ "Estimate",
      stat_type == "se." ~ "SE"
    ),
    parameter = case_when(
      parameter == "intercept" ~ "Intercept",
      parameter == "ses" ~ "SES"
    )
  ) %>%
  pivot_wider(
    names_from = stat_type,
    values_from = value
  ) %>%
  select(SiteName, parameter, Estimate, SE) %>%
  mutate(
    t_value = Estimate / SE,
    conf.low = Estimate - 1.96 * SE,
    conf.high = Estimate + 1.96 * SE,
    p_value = 2 * pt(abs(t_value), n_dfs, lower.tail = FALSE),
    p_value = ifelse(p_value < 0.001, "<0.001", round(p_value, 3))
  )

# przekształć dla wykresu
log_for_plot <- log_reshaped %>%
  filter(parameter == "SES") %>%
  select(SiteName, Estimate, SE, conf.low, conf.high) %>%
  mutate(
    color = ifelse(Estimate < 0, "#377EB8", "#E41A1C")
  )

# przekształć dla tabeli html
log_reshaped <- log_reshaped %>%
  mutate(
    SiteName = ifelse(duplicated(SiteName), "", SiteName)
  )

# plot html table
kable(log_reshaped,
  digits = 2,
  col.names = c("Site", "Parameter", "Estimate", "Std. Error", "t value", "lower CI", "upper CI", "p-value"),
  align = c("l", "l", "r", "r", "r", "r", "r", "r")
)

Site	Parameter	Estimate	Std. Error	t value	lower CI	upper CI	p-value
Bogota	Intercept	-2.39	0.09	-26.29	-2.57	-2.21	<0.001
	SES	0.26	0.06	4.03	0.13	0.39	<0.001
Helsinki	Intercept	-2.46	0.04	-56.73	-2.54	-2.37	<0.001
	SES	0.39	0.05	8.52	0.30	0.48	<0.001
Moscow	Intercept	-2.47	0.08	-30.98	-2.63	-2.32	<0.001
	SES	0.52	0.08	6.88	0.37	0.66	<0.001

Podobnie jak wcześniej, stworzymy wykres pokazujący ilorazy szans i 95% przedziały ufności dla związku SES z wysoką empatią według miejsca badań. Żadne z oszacowań nie przecina zera, więc efekt jest istotny we wszystkich miastach. Wszystkie oszacowania są dodatnie, więc zastosowano kolor czerwony.

# wykres oszacowań regresji logistycznej
log_for_plot %>%
  ggplot(aes(Estimate, SiteName)) +
  geom_point(aes(colour = color), size = 3) +
  geom_errorbarh(aes(xmin = conf.low, xmax = conf.high, colour = color), linewidth = 1.5, height = 0.2) + 
  geom_vline(xintercept = 0, lty = 2) +
  labs(
    x = "Oszacowanie związku SES z prawdopodobieństwem wyniku empatii\npowyżej 90 percentyla",
    y = "Miejsce"
      ) +
  scale_colour_manual(values = unique(as.character(log_for_plot[["color"]]))) +
  theme_minimal(base_size = 9) +
  theme(legend.position = "none")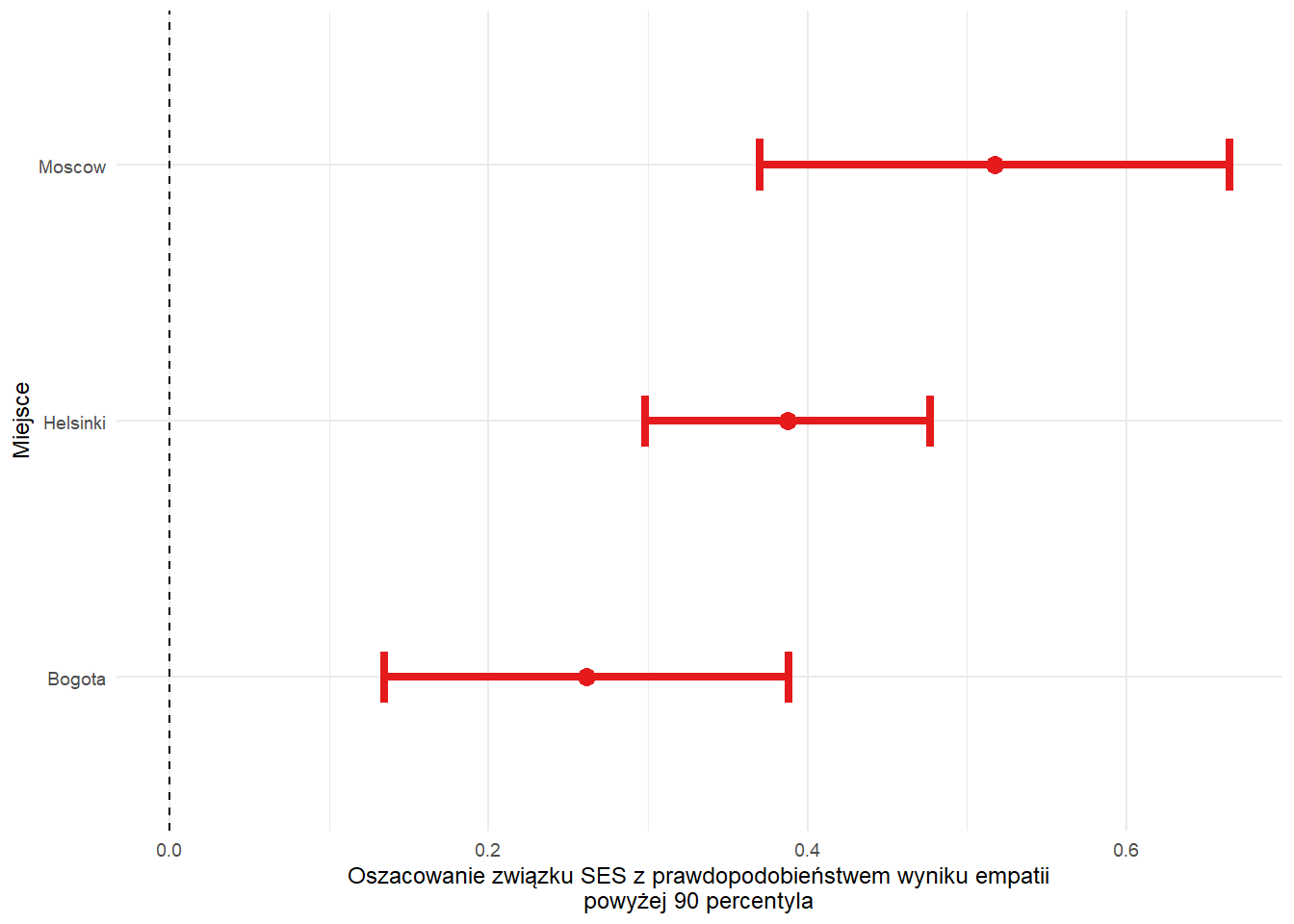

Interpretacja

W tym przypadku SES był istotnym predyktorem wysokiej empatii (powyżej 90. percentyla) we wszystkich miejscach badań. Ilorazy szans wskazują, że dla każdej jednostki wzrostu SES, szansa posiadania wysokiej empatii wzrasta około 1,30 do 1,68 razy, w zależności od miasta.

8 Podsumowanie

W tym dokumencie przedstawiliśmy, jak przygotować i analizować dane SSES 2019 przy użyciu R i pakietu Rrepest. Omówiliśmy wczytywanie danych, manipulację z użyciem dplyr oraz przeprowadzanie statystyk opisowych i analiz regresji z uwzględnieniem złożonej struktury edukacyjnego badania międzynarodowego. Wyniki dostarczyły wglądu w różnice w samokontroli według miejsca badania, płci i kohorty wiekowej, a także w związek między statusem społeczno-ekonomicznym a wysoką empatią.