library(intsvy) # do złożonych analiz badawczych
library(dplyr) # do manipulacji danymi
library(tidyr) # do przekształcania danych
library(knitr) # do tworzenia ładnych tabel HTML
library(ggplot2) # do wizualizacji danych
# Ustaw ścieżkę do katalogu z danymi
data_path <- "data/PISA/"Analiza danych PISA z pakietem intsvy
Ocena różnic w zależności od płci i kraju na umiejętności rozumienia czytanego tekstu; różnice w zależności od kraju i lokalizacji szkoły ucznia na umiejętności w zakresie nauk przyrodniczych; oraz ocena związku statusu społeczno-ekonomicznego z prawdopodobieństwem nieobecności w szkole przez ponad 3 miesiące z powodu problemowych zachowań. W poradniku wykorzystano statystyki opisowe oraz analizy regresji liniowej i logistycznej.
1 Wprowadzenie
W tej analizie przedstawiamy proces przygotowania i analizy danych z badania PISA 2022 z wykorzystaniem pakietu intsvy w R. Analiza została opracowana z myślą o użytkownikach programu R, którzy poszukują narzędzia automatycznie obsługującego międzynarodowe badania edukacyjne oraz zainteresowanych łatwą wizualizacją wyników analiz. Z tego opracowania dowiesz się:
- jak porównać wyniki uczniów w zakresie rozumienia czytanego tekstu z wybranych krajów uczestniczących w badaniu w podziale na płeć,
- jak przeprowadzić analizę różnic między wynikami uczniów w zakresie rozumowania w naukach przyrodniczych w zależności od wielkości miejscowości, w której zlokalizowana - jest szkoła ucznia, a także płci ucznia,
- jak przeprowadzić analizę zależności między statusem społeczno-ekonomicznym rodziny ucznia, a nieobecnością w szkole przez ponad trzy miesiące z powodu zachowań problemowych.
Adnotacja
Więcej informacji o pakiecie intsvy można znaleźć w naszym poradniku.
2 Konfiguracja
Najpierw załadujemy wymagane pakiety i skonfigurujmy środowisko:
3 Pobieranie, wczytywanie i przygotowanie danych
Pobieranie danych
Dane można pobrać z publicznego repozytorium danych PISA.
Należy pobrać dane w formacie .sav (format danych SPSS) i zapisać je w wybranym katalogu.
Funkcja select.merge() z pakietu intsvy przyjmuje tylko pliki .sav.
Zmienne, na których się skupimy to:
ST004D01T- płeć uczniaCNT- nazwa krajuESCS- wskaźnik statusu społeczno-ekonomicznegoSC001Q01TA- wielkość miejscowości, w której zlokalizowana jest szkołaST261Q02JA- nieobecność w szkole powyżej 3 miesięcy (np.z powodu przemocy, używania lub sprzedawania narkotyków) [Tak/Nie]PV1READdoPV10READ- wartości prawdopodobne wyników rozumienia czytanego tekstuPV1SCIEdoPV10SCIE- wartości prawdopodobne wyników zakresu rozumowania w naukach przyrodniczych
Użyjemy funkcji pisa.select.merge() do wczytania i połączenia zbiorów danych uczniów i szkół. Skupimy się na czterech krajach: Maroko, Finlandia, Singapur i Polska.
pisa22 <- pisa.select.merge(
folder = data_path,
school.file = "CY08MSP_SCH_QQQ.SAV",
student.file = "CY08MSP_STU_QQQ.SAV",
student = c("ESCS", "ST004D01T", "ST261Q02JA"),
school = c("SC001Q01TA"),
countries = c("Finland", "Poland", "Singapore", "Morocco")
)Mamy gotowy zbiór danych do analizy. Przejdźmy dalej.
4 Różnice w wynikach rozumienia czytanego tekstu według kraju i płci
W tej części porównamy średnie i odchylenia standardowe wyników rozumienia czytanego tekstu według kraju i płci.
Średnia i odchylenie standardowe z rozumienia czytanego tekstu według kraju i płci
# Średnie wyniki z rozumienia czytanego tekstu według kraju i płci w PISA
descriptives <- pisa.mean.pv(
pvlabel = paste0("PV", 1:10, "READ"),
by = c("CNT", "ST004D01T"),
data = pisa22
)
kable(descriptives,
digits = 2,
col.names = c("Country", "Gender", "N", "Mean", "Mean s.e.", "SD", "SD s.e."),
align = c("l", "l", "r", "r", "r", "r", "r")
)| Country | Gender | N | Mean | Mean s.e. | SD | SD s.e. |
|---|---|---|---|---|---|---|
| Finland | Female | 4995 | 513.01 | 2.57 | 97.40 | 1.45 |
| Finland | Male | 5244 | 468.32 | 2.77 | 105.49 | 1.36 |
| Morocco | Female | 3401 | 350.37 | 3.94 | 73.63 | 1.97 |
| Morocco | Male | 3466 | 328.65 | 4.21 | 76.01 | 2.15 |
| Poland | Female | 3009 | 503.24 | 3.25 | 98.09 | 2.06 |
| Poland | Male | 3002 | 474.60 | 3.20 | 107.56 | 2.54 |
| Singapore | Female | 3248 | 552.55 | 2.28 | 101.74 | 1.42 |
| Singapore | Male | 3358 | 532.95 | 2.21 | 108.87 | 1.85 |
Pakiet intsvy posiada wbudowane funkcje do tworzenia wykresów dla statystyk opisowych i można ich użyć do wizualizacji wyników.
Umożliwia niewielkie dostosowania wykresów.
desc_plot <- plot.intsvy.mean(descriptives)
desc_plot[["labels"]][["colour"]] <- "Gender"
desc_plot[["labels"]][["x"]] <- "Country"
desc_plot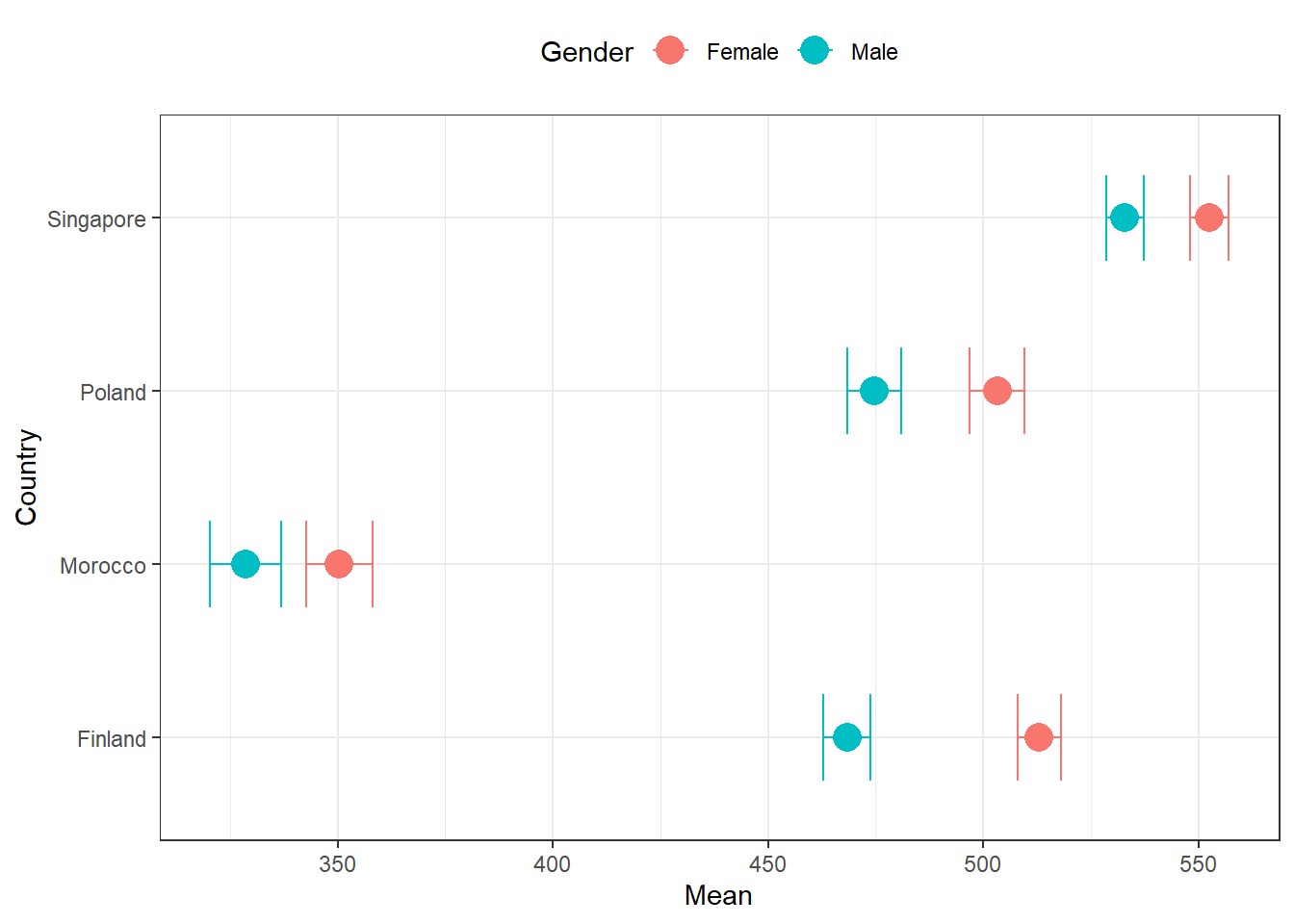
5 Czy umiejętności w zakresie rozumowania w nauk przyrodniczych różnią się w zależności od wielkości miejscowości, w której znajduje się szkoła?
Na to pytanie odpowiemy za pomocą regresji liniowej, gdzie nauki przyrodnicze będą zmienną zależną, a wielkość miejscowości zmienną niezależną. Kategoria “wieś, osada lub obszar wiejski (mniej niż 3000 mieszkańców)” będzie kategorią referencyjną.
Rekodowanie zmiennej wielkości miejscowości
Zmienna wielkość miejscowości (SC001Q01TA) ma bardzo długie nazwy kategorii.
Dodamy etykiety do tej zmiennej, żeby uzyskać bardziej czytelne wyniki.
kable(with(pisa22, table(SC001Q01TA)))| SC001Q01TA | Freq |
|---|---|
| A village, hamlet or rural area (fewer than 3 000 people) | 2198 |
| A small town (3 000 to about 15 000 people) | 3059 |
| A town (15 000 to about 100 000 people) | 7538 |
| A city (100 000 to about 1 000 000 people) | 8223 |
| A large city (1 000 000 to about 10 000 000 people) | 8003 |
| A megacity (with over 10 000 000 people) | 380 |
pisa22[["SC001Q01TA"]] <- factor(pisa22[["SC001Q01TA"]],
levels = c("A village, hamlet or rural area (fewer than 3 000 people)",
"A small town (3 000 to about 15 000 people)",
"A town (15 000 to about 100 000 people)",
"A city (100 000 to about 1 000 000 people)",
"A large city (1 000 000 to about 10 000 000 people)",
"A megacity (with over 10 000 000 people)"),
labels = c(" Rular <3k",
" Small town 3k-15k",
" Town 15k-100k",
" City 100k-1M",
" Large city 1M-10M",
" Megacity >10M")
)Uruchomienie modelu regresji liniowej
Istotność wyników
Aby określić, czy predyktor jest istotny, należy wziąć pod uwagę wartości t w wynikach regresji.
Wartości t większe niż 1,96 (w wartości bezwzględnej) wskazują, że predyktor jest statystycznie istotny na poziomie istotności 0,05.
Alternatywnie możemy obliczyć wartość p z wartości t używając następującego wzoru:
wartość p = 2 * (1 - pt(abs(wartość t), df)) gdzie df to liczba wag replikacyjnych minus liczba parametrów do oszacowania.
# Związek lokalizacji szkoły i umiejętności w zakresie nauk przyrodniczych
city_lm <- pisa.reg.pv(
pvlabel = paste0("PV", 1:10, "SCIE"),
x = c("SC001Q01TA"),
data = pisa22
)
# ustaw df do obliczania wartości p
# 80 wag replikacyjnych - 1 (stała) - 5 poziomów czynnika (6-1 (referencja))
dfs <- 80 - 1 - (length(levels(pisa22[["SC001Q01TA"]])) - 1)
city_lm_tab <- city_lm[["reg"]]
city_lm_tab[["p-value"]] <- 2 * (1 - pt(abs(city_lm_tab[["t value"]]), dfs))
city_lm_tab[["p-value"]] <- ifelse(city_lm_tab[["p-value"]] < 0.001,
"<0.001",
round(city_lm_tab[["p-value"]], 3)
)
rownames(city_lm_tab) <- c("Intercept", levels(pisa22[["SC001Q01TA"]])[-1], "R²")
kable(city_lm_tab,
digits = 2,
col.names = c("Variable", "Estimate", "Std. Error", "t-value", "p-value"),
align = c("l", "r", "r", "r", "r")
)| Variable | Estimate | Std. Error | t-value | p-value |
|---|---|---|---|---|
| Intercept | 366.81 | 5.78 | 63.47 | <0.001 |
| Small town 3k-15k | 58.93 | 10.39 | 5.67 | <0.001 |
| Town 15k-100k | 84.18 | 8.27 | 10.19 | <0.001 |
| City 100k-1M | 84.70 | 9.42 | 8.99 | <0.001 |
| Large city 1M-10M | 86.85 | 11.04 | 7.87 | <0.001 |
| Megacity >10M | 15.90 | 19.37 | 0.82 | 0.414 |
| R² | 0.07 | 0.01 | 5.36 | <0.001 |
Pakiet intsvy umożliwia tworzenie wykresów współczynników regresji w ograniczonym zakresie.
Jednak aby stworzyć wykres regresji z predyktorem kategorialnym o kilku poziomach, musimy użyć innego pakietu, takiego jak ggplot2.
Najpierw musimy obliczyć przedziały ufności i dodać kolumnę z kolorem w zależności od kierunku efektu.
city_lm_plot <- city_lm_tab %>%
mutate(
conf.low = Estimate - 1.96 * `Std. Error`,
conf.high = Estimate + 1.96 * `Std. Error`,
color = ifelse(Estimate < 0, "#377EB8", "#E41A1C"),
city = factor(rownames(city_lm_tab), levels = rev(levels(pisa22[["SC001Q01TA"]])[-1]))
) %>%
filter(city != "Intercept" & city != "R²")
city_lm_plot %>%
ggplot(aes(Estimate, city)) +
geom_point(aes(colour = color), size = 3) +
geom_errorbarh(aes(xmin = conf.low, xmax = conf.high, colour = color), linewidth = 1.5, height = 0.2) +
geom_vline(xintercept = 0, lty = 2) +
labs(
x = "Wyniki w naukach przyrodniczych\nw porównaniu do terenów wiejskich (<3k mieszkańców)",
y = "Wielkość miejscowości, w której znajduje się szkoła"
) +
scale_colour_manual(values = unique(as.character(city_lm_plot[["color"]]))) +
theme_minimal(base_size = 10) +
theme(legend.position = "none")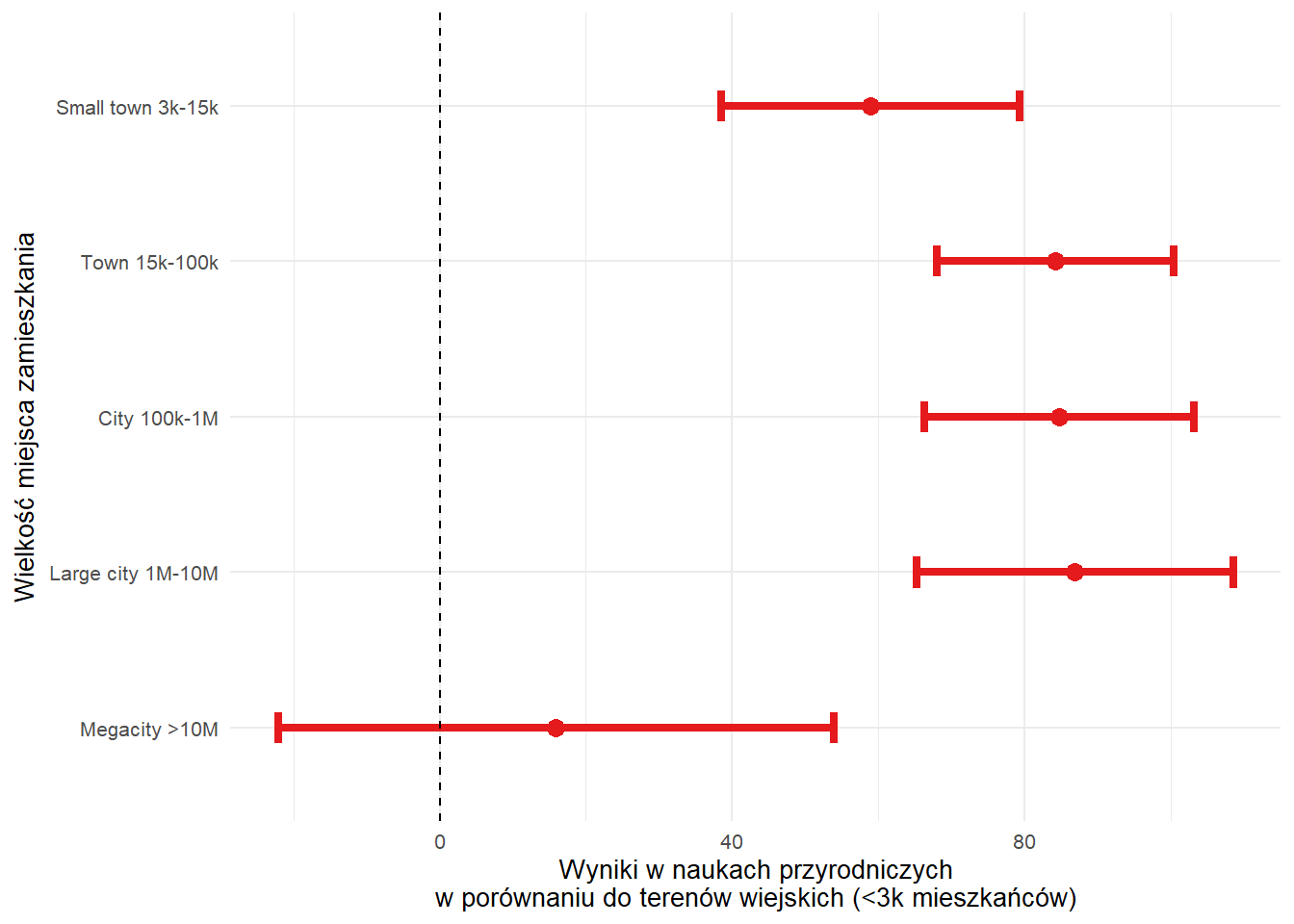
6 SES jako predyktor nieobecności w szkole przez ponad 3 miesiące z powodu zachowań problemowych
W tej części użyjemy regresji logistycznej do sprawdzenia, czy status społeczno-ekonomiczny (SES) przewiduje prawdopodobieństwo nieobecności w szkole przez ponad 3 miesiące z powodu zachowań problemowych.
Tabela krzyżowa dla kraju i interesującej nas zmiennej
Na początku spojrzymy na tabelę krzyżową dla kraju i zmiennej będącej przedmiotem zainteresowania (ST261Q02JA).
cross_tab <- with(pisa22, table(CNT, ST261Q02JA))
kable(cross_tab, digits = 2,
col.names = c("Country", "Yes, n", "No, n")
)| Country | Yes, n | No, n |
|---|---|---|
| Finland | 34 | 250 |
| Morocco | 116 | 812 |
| Poland | 29 | 264 |
| Singapore | 18 | 272 |
prop_tab <- prop.table(cross_tab, margin = 1) * 100
kable(prop_tab, digits = 2,
col.names = c("Country", "Yes, %", "No, %")
)| Country | Yes, % | No, % |
|---|---|---|
| Finland | 11.97 | 88.03 |
| Morocco | 12.50 | 87.50 |
| Poland | 9.90 | 90.10 |
| Singapore | 6.21 | 93.79 |
Odsetek uczniów, którzy opuścili szkołę na 3 lub więcej miesięcy z powodu zachowań problemowych jest stosunkowo niski we wszystkich krajach, ale są zauważalne różnice.
Singapur ma najniższy odsetek (6,2%), podczas gdy w Maroku odsetek ten jest najwyższy (12,5%).
Niemniej jednak chcemy zbadać, czy SES przewiduje zachowania problemowe w tych 4 krajach.
Uruchomienie modelu regresji logistycznej
# Prawdopodobieństwo nieobecności w szkole z powodu zachowań problemowych według SES
escs_log <- pisa.log(
y = "ST261Q02JA",
x = "ESCS",
by = "CNT",
data = pisa22
)
# ustaw df do obliczania wartości p
# 80 wag replikacyjnych - 1 (stała) - 1 (predyktor)
dfs_log <- 80 - 1 - 1
escs_all_log <- do.call(rbind, list(escs_log[["Finland"]][["reg"]],
escs_log[["Morocco"]][["reg"]],
escs_log[["Poland"]][["reg"]],
escs_log[["Singapore"]][["reg"]]
)
)
escs_all_log[["p-value"]] <- 2 * (1 - pt(abs(escs_all_log[["t value"]]), dfs_log))
escs_all_log[["p-value"]] <- ifelse(escs_all_log[["p-value"]] < 0.001,
"<0.001",
round(escs_all_log[["p-value"]], 3)
)
rownames(escs_all_log) <- paste0(rep(c("Finland", "Morocco", "Poland", "Singapore"), each = 2), c(" Intercept", ""))
kable(escs_all_log,
digits = 2,
col.names = c("Variable","Estimate", "Std. Error", "t-value", "Odds Ratio", "lower CI95", "upper CI95", "p-value"),
row.names = TRUE,
align = c("l", "r", "r", "r", "r", "r", "r", "r")
) | Variable | Estimate | Std. Error | t-value | Odds Ratio | lower CI95 | upper CI95 | p-value |
|---|---|---|---|---|---|---|---|
| Finland Intercept | 2.11 | 0.26 | 8.11 | 8.28 | 4.97 | 13.80 | <0.001 |
| Finland | -0.49 | 0.21 | -2.32 | 0.61 | 0.40 | 0.93 | 0.023 |
| Morocco Intercept | 1.27 | 0.16 | 7.91 | 3.56 | 2.60 | 4.88 | <0.001 |
| Morocco | -0.45 | 0.08 | -5.47 | 0.64 | 0.54 | 0.75 | <0.001 |
| Poland Intercept | 2.24 | 0.25 | 8.87 | 9.36 | 5.71 | 15.35 | <0.001 |
| Poland | -0.05 | 0.40 | -0.12 | 0.95 | 0.44 | 2.07 | 0.904 |
| Singapore Intercept | 2.98 | 0.28 | 10.49 | 19.72 | 11.29 | 34.42 | <0.001 |
| Singapore | 0.56 | 0.27 | 2.07 | 1.74 | 1.03 | 2.95 | 0.041 |
Podobnie jak w przypadku wykresu regresji liniowej, dla regresji logistycznej również musimy przygotować wykres samodzielnie używając ggplot2
escs_log_plot <- escs_all_log %>%
mutate(
conf.low = `Coef.` - 1.96 * `Std. Error`,
conf.high = `Coef.` + 1.96 * `Std. Error`,
color = ifelse(`Coef.` < 0, "#377EB8", "#E41A1C"),
country = rownames(escs_all_log)
) %>%
filter(!(endsWith(country, "Intercept")))
escs_log_plot %>%
ggplot(aes(`Coef.`, country)) +
geom_point(aes(colour = color), size = 3) +
geom_errorbarh(aes(xmin = conf.low, xmax = conf.high, colour = color), linewidth = 1.5, height = 0.2) +
geom_vline(xintercept = 0, lty = 2) +
labs(
x = "Związek z nieobecnością w szkole >3 miesięcy\n ze względu na zachowania problemowe",
y = "Kraj"
) +
scale_colour_manual(values = unique(as.character(escs_log_plot[["color"]]))) +
theme_minimal(base_size = 10) +
theme(legend.position = "none")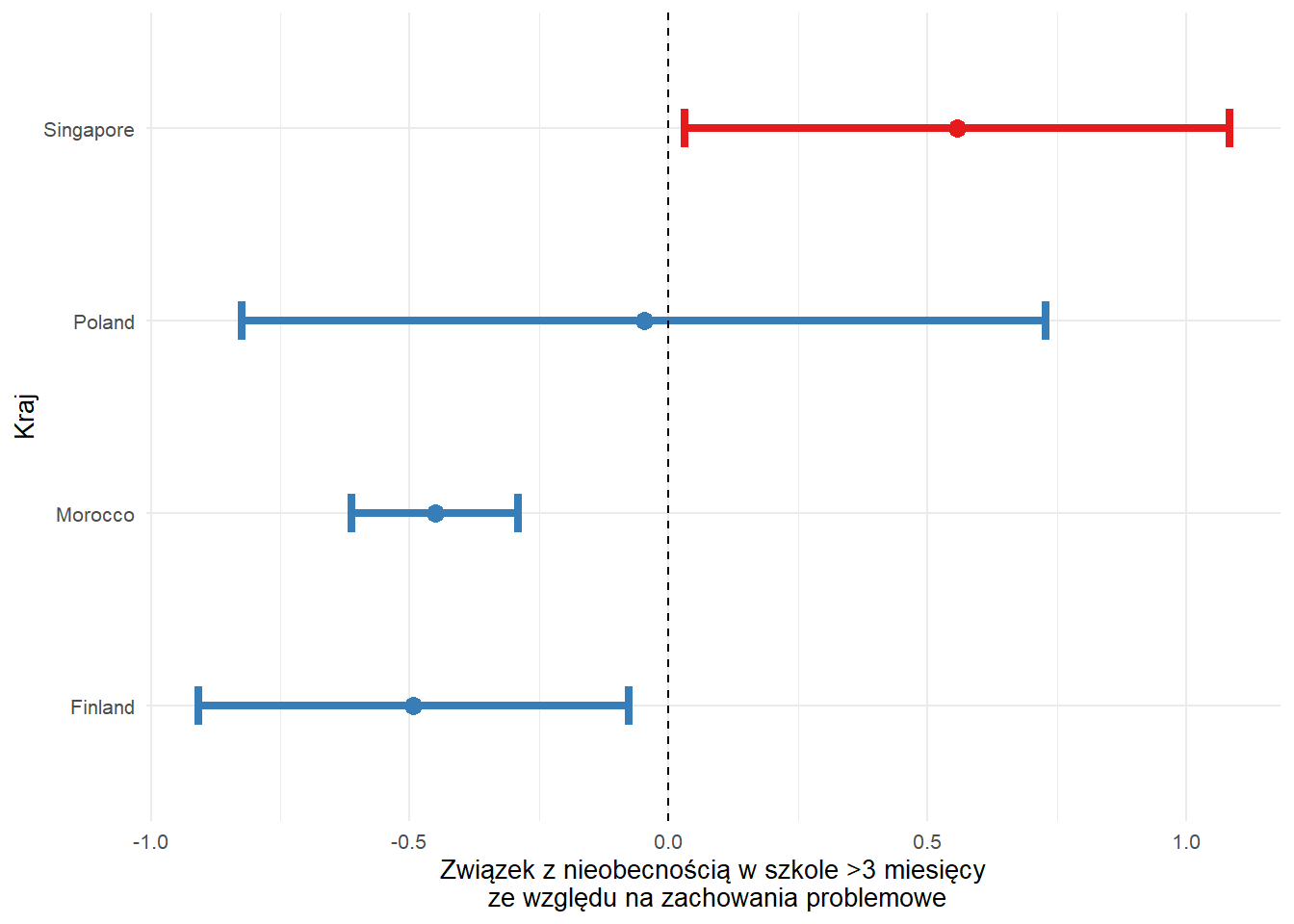
7 Podsumowanie
W tym poradniku przedstawiono, jak przygotować i analizować badanie PISA 2022 za pomocą pakietu R intsvy. Omówiliśmy wczytywanie i łączenie danych oraz obliczenie statystyk opisowych i analiz regresji z uwzględnieniem złożonego schematu badania. Wyniki dostarczyły wglądu w różnice umiejętności czytania według kraju i płci. Następnie zbadaliśmy związek między wielkością miejscowości szkoły a umiejętnościami w zakresie nauk przyrodniczych. Na koniec zbadaliśmy związek statusu społeczno-ekonomicznego z prawdopodobieństwem opuszczenia szkoły z powodu zachowań problemowych.